Parametric Weighted Automata

12 Apr 2019
Joshua Moerman

I moved to Aachen for a post-doc on probabilistic programs (see FRAPPANT). This means that I am learning about new, exciting topics. I will collect notes on this blog, as they may be useful to others. One of the research lines here is that of parametric Markov chains, see for example Parameter Synthesis for Markov Models: Faster Than Ever and references therein.

Parametric Markov chains are just like Markov chains, except that they allow for unspecified, or parametric edges. Instead of a precise probability, these edges will have a formal parameter $p$ . To make life a bit easier, I generalise from probabilities in $[0, 1]$ to any value in $R$ . So in this post, I talk about parametric weighted finite automata (pWFAs). I will do this for a single parameter $p$ , but it all generalises nicely to multiple parameters.

Example Let’s start with an example, before we define pWFAs. The image below defines a pWFA with two states: $q_{0}$ (initial) and $q_{1}$ which have the outputs $o (q_{0}) = 0$ and $o (q_{1}) = 1 - p$ respectively. We have a single letter $a \in Σ$ in our alphabet. On this letter, the state $q_{0}$ transitions to $q_{0}$ with weight $p$ and to $q_{1}$ with weight $1$ . State $q_{1}$ simply transitions to itself with weight $1$ . (If there is just a single transition with unit weight, we often simplify the labels in the picture.)

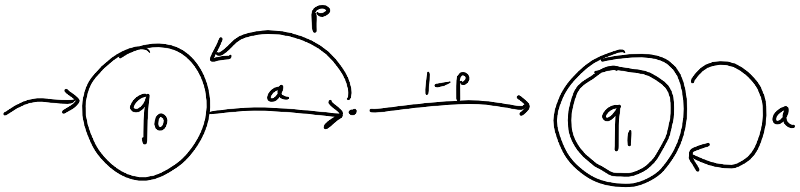
Example pWFA

What is the acceptance of – say – the word $aa$ ? In total there are three paths: $q_{0} \to q_{0} \to q_{0}$ , $q_{0} \to q_{0} \to q_{1}$ , and $q_{0} \to q_{1} \to q_{1}$ with the respective weights $p \cdot p \cdot 0$ , $p \cdot (1 - p) \cdot 1$ , and $(1 - p) \cdot (1 - p) \cdot 1$ . Summing these up, gives an acceptance of $1 - p^{2}$ . This polynomial can evaluated for any $p \in R$ .

Let us fix an alphabet $Σ$ .

Definition A parametric weighted finite automaton, $A$ , consists of

a state space: a finite set $Q$ ,
an initial vector: an element $i \in R ⟨ Q ⟩$ ,
an output function: a map $o : Q \to R$ , and
transition functions: for each $a \in Σ$ we have a map $δ_{a} : Q \times Q \to R [p]$ .

Let me explain the notation: $R ⟨ Q ⟩$ is the free $R$ -vector space with $Q$ as a basis. As a set it is $R ⟨ Q ⟩ = R^{Q} = {f : Q \to R}$ , but we think of the elements $v \in R ⟨ Q ⟩$ as formal sums $v = \sum_{q} r_{q} \cdot q$ for some values $r_{q} \in R$ . So the initial vector $i$ is really a linear combination of states. In the example above, the initial vector is the state $q_{0}$ with weight $1$ .

In the transition function we see $R [p]$ , which is the polynomial ring with indeterminate $p$ . (It is also a free vector space, but with a basis $1, p, p^{2}, \dots$ ) This allows transitions to use normal weights from $R$ , but also polynomials involving $p$ . The weight is $δ_{a} (q, q^{'}) = 0$ if there is no $a$ -transition from $q$ to $q^{'}$ . The maps $δ_{a}$ can be equivalently defined as $δ_{a} : Q \to R [p] ⟨ Q ⟩$ . (This is the free $R [p]$ -module on $Q$ .) Going further, it can be equivalently expressed as a $R$ -linear map $δ_{a} : R ⟨ Q ⟩ \to R [p] ⟨ Q ⟩$ , or even a $R [p]$ -linear map. All these manipulations are one-to-one, and I will switch to whatever is useful in the context.

We can do the same for the output map. It is equivalently defined as a linear map $o : R [p] ⟨ Q ⟩ \to R [p]$ , i.e., it is a dual vector $o \in R [p] ⟨ Q ⟩^{*}$ .

Example To see why these equivalent characterisations matter, we can compute the example from above:

o (δ_{a} (δ_{a} (i))) = o (δ_{a} (δ_{a} (q_{0}))) = o (δ_{a} (p \cdot q_{0} + (1 - p) \cdot q_{1})) = o (p \cdot δ_{a} (q_{0}) + (1 - p) \cdot δ_{a} (q_{1})) = o (p^{2} \cdot q_{0} + (1 - p) p \cdot q_{1} + (1 - p) \cdot q_{1}) = p^{2} \cdot o (q_{0}) + (p - p^{2} + 1 - p) \cdot o (q_{1}) = 1 - p^{2} .

I have used linearity in many of these steps.

Applications

Why do we bother with all this? We often use Markov chains in model checking, and typically we want to compute things like “what is the probability that something good eventually happens?” But how do we actually obtain a Markov chain in the first place? Some engineer, or domain expert, will design it and has to justify why it models reality. It may be easier to leave some edges unspecified, by using a parameter. Luckily, as we will see, we can still do model checking for parametrised systems. This probability will then, of course, depend on the parameter. So instead of a single value, we obtain a function from the model checker.

I will not be precise in the type of properties we can model check. But I will assume that “good” states are states with an output $1$ , and that good states have no outgoing edges (once we are in a good state, we stay there).

Disclaimer You can imagine that for general weighted automata, the outcome may not be a probability (a value in $[0, 1]$ ). We will need all the weights to sum up to $1$ , and we need bounds on $p$ , etc. We ignore well-definedness in this post and pretend everything is fine.

The probability of reaching a good state is the sum over all paths leading to a good state:

outcome = w \in Σ^{*} \sum o (δ_{w} (i)) .

Here I have abbreviated $δ_{a_{1} \dots a_{k}} = δ_{a_{k}} \circ \dots \circ δ_{a_{1}}$ . Let’s keep our fingers crossed and hope that this sum converges. (“Mathematics is wishful thinking” - Wim Veldman.) How can we compute it?

We first generalise this quantity to any state:

v (q) = w \sum o (δ_{w} (q)) .

Then, by unrolling the transition function once, we see:

v (q) = o (q) + a \sum v (δ_{a} (q)),

where I’ve silently extended $v$ linearly.

Now we manipulate this equation, first we write it as a composition (again using linearity to push the sum inwards):

v (q) = o (q) + (v \circ a \sum δ_{a}) (q) .

Then, let’s get rid of $q$ , and keep the linear functions. We might as well write the composition as a matrix multiplication.

v = o + v \times a \sum δ_{a} .

Put things to the other side (here $1$ is the identity matrix).

o = v \times (1 - a \sum δ_{a}) .

And, finally, transpose and rename:

A v^{T} = o^{T},

where the matrix $A = 1 - \sum_{a} δ_{a}^{T}$ .

So, we see that we can compute $v (i)$ , the value that we are interested in, by solving a linear system of equations! Wait, what? Is that really all there is to it? Well, we have cheated a bit, the maps $δ_{a}$ live in a $R [p]$ -linear space. This is not a field, and so we cannot expect to just solve this equation. Can we even ask for a map $v : R [p] ⟨ Q ⟩ \to R [p]$ ?

There is a way out: Consider the field of fractions $R (p)$ . This is the set of rational functions $\frac{f}{g}$ , where $f$ and $g$ are polynomials. This is a field which extends the polynomial ring, and so we can solve the equation here. One can solve it with, for example, Guassian elimination, which is very similar to state elimination. (Side note: value iteration will not work in such a field, I believe.)

In the end we find that the probability of eventually ending up in a good state is not a polynomial in $p$ . Rather, it is a rational function. I find it cool, that we can derive this with pure linear algebra. Although, this derivation seems easy, of course it hinges on the assumption that a solution exists, a fact which has to be shown separately. Also note that we can do this with $Q$ as our base field, instead of $R$ , in order to do this numerically exact.

Sebastian Junges has implemented such a tool (together with colleagues at RWTH Aachen) and has a nice slide (see s. 41) where he shows that these rational functions can be monstrous expressions. I would like to thank Jip Spel to introduce me to the basics of parametric Markov chains.

Learning

In a subsequent post, I hope to talk a bit about (active) learning of parametric weighted automata. Stay tuned!

I used to have a Disqus comments section here. But everybody seems to simply send me emails instead. I have disabled Disqus, in order to avoid third-party trackers.